7564. Расстояние на триангуляции

 

Имеется правильный многоугольник. Вершины многоугольника последовательно пронумерованы числами от 1 до n. Имеется также триангуляция этого многоугольника, заданная списком из n − 3 диагоналей.

Заданы q запросов. Каждый запрос задается номерами двух вершин. Для каждого запроса найдите кратчайшее расстояние между этими двумя вершинами, двигаясь по сторонам или заданным диагоналям многоугольника, расстояние равно общему количеству пройденных сторон и диагоналей.

 

Вход. Первая строка содержит количество вершин в многоугольнике n (4 ≤ n ≤ 50 000).

Каждая из следующих n – 3 строк содержит два числа ai, bi – концы i-ой диагонали (1 ≤ ai, bi ≤ n, ai ≠ bi).

Следующая строка содержит количество запросов q (1 ≤ q ≤ 100 000).

Каждая из следующих q строк содержит два целых числа xi, yi (1 ≤ xi, yi ≤ n) – вершины i-го запроса. Гарантируется, что никакая диагональ не совпадает со стороной многоугольника и никакие две диагонали не совпадают и не пересекаются.

 

Выход. Для каждого запроса выведите в отдельной строке кратчайшее расстояние.

 

Пример входа

Пример выхода

6

1 5

2 4

5 2

5

1 3

2 5

3 4

6 3

6 6

2

1

1

3

0

 

 

РЕШЕНИЕ

геометрия – рекурсия, разделяй и властвуй

 

Анализ алгоритма

В любом триангулированном многоугольнике существует диагональ, которая отрезает от многоугольника минимум n / 3 вершин. Найдем диагональ (i, j), которая делит многоугольник на две части, модуль разницы количества вершин в которых минимален. Это будет такая диагональ (i, j), что расстояние от i до j по периметру многоугольника будет наибольшей. Выбор диагонали  произвольным образом даст Time Limit.

При помощи поиска в ширину за O(n) найдем кратчайшие расстояния от i и от j до всех вершин по сторонам и диагоналям многоугольника.

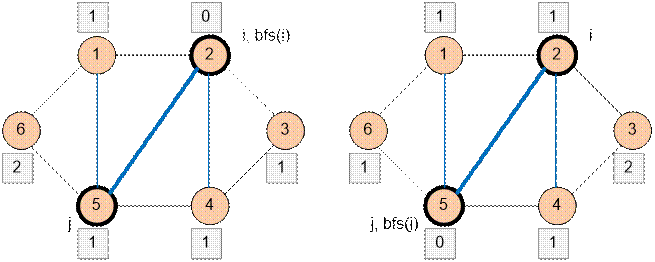
Разделим многоугольник на два по выбранной диагонали.Далее снова ищем в каждом из них диагональ, делящую по возможности пополам, с обоих концов диагоналей запускаем поиск в ширину и снова продолжаем делить многоугольники по диагонали. Процесс деления продолжаем, пока многоугольник не станет треугольником (не будет внутри себя содержать диагоналей триангуляции).

Глубина рекурсии составит O(log2n), в результате разрезаний получим O(n) многоугольников общего размера O(n log2n).

 

Рассмотрим запрос (x, y) – поиск кратчайшего расстояния от x до y. Если вершины запроса лежат по одну сторону от разделяющей диагонали (i, j), то решаем задачу в соответствующем многоугольнике. В противном случае кратчайший путь dist(x, y) от x до y обязательно будет проходить либо через i, либо через j. То есть

dist(x, y) = min (dist(x, i) + dist(i, y), dist(x, j) + dist(j, y))

Все расстояния в правой части равенства нам известны – мы их нашли поиском в ширину.

 

Пример

 

 

 

 

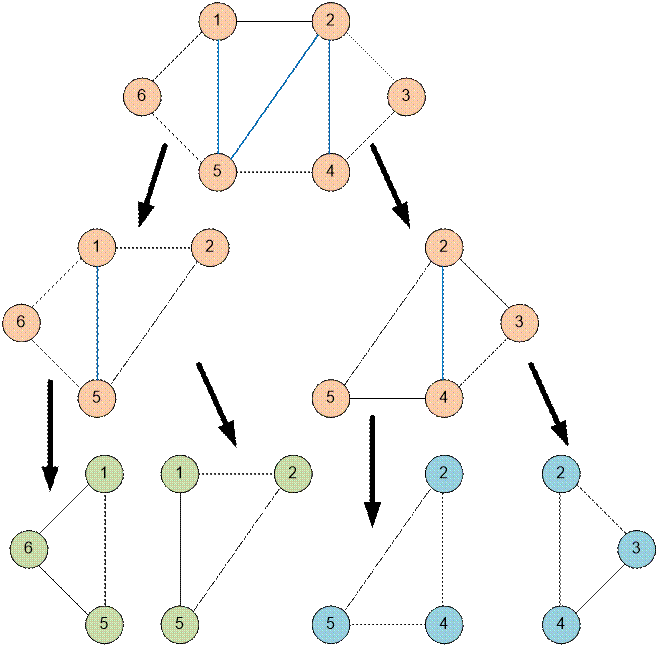
Реализация алгоритма